Original Articles: 2021 Vol: 13 Issue: 9
Quantum Chemical Prediction of Redox Potential Apply to Phenolic Derivatives
Chabi Doco R*, Kpota Houngue MTA, Koudjina S, Kpotin GA, Atohoun YGS
Department of Chemistry, Laboratory of Theoretical Chemistry and Molecular Spectroscopy, Cotonou, Benin
Abstract
Reliable prediction of oxidation-reduction potential in phenolic compounds involves determination of quantum and molecular descriptors. In this work, the redox potential of set of thirty-one (31) molecules was determined using seven different quantum descriptors and one molecular descriptor. The calculations, performed at the SWN/6- 31G, HF/6-31G and AM1 theory level allowed us to establish the Quantitative Structure-Property Relationship (QSPR) analysis of substituted phenols that can predict redox potential with confidence level of over 95%.
Keywords
Redox potential; Theory level; Phenols; QSPR
Introduction
Phenolic compounds are of great interest because of their involvement in biological and industrial processes. They have important biological activities (anticancer, antioxidant, anti-cardiovascular and anti-inflammatory). Several studies have shown that hydroxyl groups of these compounds are essential in free radicals trapping. Recent theoretical works have shown existence of several quantum descriptors that can predict antioxidant properties of these bioactive molecules [1-5]. In addition, the work of Steenken, et al., Jovanovic et al., have shown that redox potential is an important experimental parameter for elucidating and comparing antioxidant powers of phenol derivatives as well as that of hydroxyl groups on the flavonoids ring system [4,5].
The goal of our work is to develop models for predicting redox potential by SWN/6-31G, HF/6-31G and AM1 theory level. For this, appropriate descriptors will be selected from a set of seven quantum descriptors and a molecular descriptor, taking into account only those that are highly correlated with redox potential while being independent of each other. The results of this work will make it possible to establish and validate by a statistical method efficient QSPR models [2].
Materials and Methods
Thirty-one (31) phenolic compounds whose experimental values of redox potential E are known were selected in the literature and form the structural basis of our study. These phenolic compounds are divided in two groups or sets: the training set containing 21 molecules (≈ 2/3 of the base molecules) and the test set containing 10 molecules (≈ 1/3 of the basis molecules). The choice of molecules for the constitution of groups is arbitrary. Molecules are codified Fi in order to simplify their notations [3] (Table 1).
| Code | Compounds | Code | Compounds |
|---|---|---|---|
| F1 | 4-NO2 | F17 | 2-OCH3-4-CH3 |
| F2 | 4-CN | F18 | 3, 4-(CH3O)2 |
| F3 | 4-I | F19 | 3, 4,5-(CH3O)3 |
| F4 | 4-COCH3 | F20 | Sesamol |
| F5 | 4-COOH | F21 | 2-OH-4-COOH |
| F6 | 4-H | F22 | 2, 6-(CH3O)2 |
| F7 | 4-Br | F23 | 2, 3-(OH)2 |
| F8 | 4-Cl | F24 | 2,3-(OH)2-5-COOCH3 |
| F9 | 4-F | F25 | 3,4-Dihydroxycinnamic acid |
| F10 | Tyrosine | F26 | 2-OH |
| F11 | 3-OH-4-COCH3 | F27 | 2-OH-4-CH3 |
| F12 | 4-CH3 | F28 | α-Tocopherol |
| F13 | 3,5-(CH3O)2 | F29 | 4-OH |
| F14 | 3-OH-5-OCH3 | F30 | 4-NH2 |
| F15 | 3-OH | F31 | 4-(CH3)3 |
| F16 | 4-OCH3 |
Table 1: Structure of phenolic compounds
All molecules were optimized using SWN/6-31G, HF/6-31G and AM1 theory level as implemented in GAUSSIAN 09 program. Two software’s XLSTAT and EXCEL have been used, according to their specificities, to conduct statistical analysis of the results and to draw the graph [4-6].
The principle of linear regression is to model a quantitative dependent variable Y through a linear combination of p quantitative explanatory variables X1, X2……Xp. The deterministic model is written as:
Y= β0+β1 X1+ β2 X2+ ……. +βp Xp+ ԑ
Where βi are coefficients of the regression and ԑ the model error. The choice of quantum descriptors is based on two fundamental criteria [7].
Criterion 1
By nature, the dependence of Y on Xi is assumed to be linear. For this, the absolute value of the linear correlation coefficient between the property Y and the variables Xi must be greater than 0.50.
|R| ≥ 0.50
Criterion 2
the different samples Yi are supposed to be independent of each other. For two descriptors i and j to be independent, the partial correlation coefficient (aij) between them must be strictly less than 0.70 [8].
aij<0.70
The predictive power of a model is also based on Tropsha criteria. If the three fifths (3/5) of the criteria are verified then the model has a good predictive power.
Criterion 1: Rext2>0.70;
Criterion 2: Qext2>0.60;
Criterion 3: (Rext2-R02)/(Rext2 )<0.1 and 0.85<k<1.15
Criterion 4: (Rext2-R0'2)/(Rext2 )<0.1 and 0.85<k’<1.15
Criterion 5: |Rext2-R02| ≤ 0.30
Normality tests have also been performed to verify the quality of the confidence interval obtained. These are Shapiro-Wilk and Durbin-Watson tests. The different expressions and the notations of the quantum descriptors used are gathered in Table 2.
| Quantum descriptors | Energy HOMO | Energy LUMO | Energy gap | Electronegativity | Hardness | Molless | Electrophily indice |
|---|---|---|---|---|---|---|---|
| Expressions | EHOMO | ELUMO | ELUMO-EHOMO | χ=(IP+EA)/2 | η=(IP-EA)/2 | S=1/(2η) | ω=χ2/2η |
Table 2: Quantum descriptors used expressed in electron volt (eV)
The HOMO and LUMO orbitals obtained on each 31 set of molecules (F1…F31) have been used to calculate the different parameters of the quantum descriptors [9-11]. This orbitals means have to make the quantum descriptor choice easier under the caster of the chemical selective methods (Figure 1).
Results and Discussion
Choice of Quantum Descriptors
Calculated values of quantum descriptors at SWN/6-31G, HF/6-31G and AM1 theory level for molecules of the learning set and their redox potentials identified in the literature are summarized (Tables 3-5).
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F1 | -0.36 | -0.07 | 0.29 | 0.2 | 0.15 | 2.94 | 0.94 | 0 | 1.23 |
| F2 | -0.34 | -0.05 | 0.29 | 0.18 | 0.16 | 2.78 | 0.11 | 0 | 1.17 |
| F3 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 0 | 1.09 |
| F4 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 0 | 1.06 |
| F5 | -0.32 | -0.05 | 0.27 | 0.17 | 0.15 | 2.94 | 0.11 | 0 | 1.04 |
| F6 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 0 | 0.97 |
| F7 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 0 | 0.96 |
| F8 | -0.32 | -0.03 | 0.29 | 0.16 | 0.16 | 2.78 | 0.09 | 0 | 0.94 |
| F9 | -0.32 | -0.03 | 0.29 | 0.16 | 0.16 | 2.78 | 0.09 | 0 | 0.93 |
| F10 | -0.32 | 0.04 | 0.28 | 0.16 | 0.16 | 2.78 | 0.08 | 0 | 0.89 |
| F11 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.09 | 1 | 0.89 |
| F12 | -0.32 | 0.04 | 0.28 | 0.15 | 0.16 | 2.78 | 0.08 | 0 | 0.87 |
| F13 | -0.3 | 0.05 | 0.25 | 0.14 | 0.16 | 2.78 | 0.07 | 0 | 0.85 |
| F14 | -0.31 | 0.04 | 0.27 | 0.15 | 0.16 | 2.78 | 0.08 | 1 | 0.84 |
| F15 | -0.3 | 0.05 | 0.25 | 0.14 | 0.15 | 2.94 | 0.08 | 1 | 0.81 |
| F16 | -0.32 | 0.04 | 0.28 | 0.16 | 0.16 | 2.78 | 0.09 | 0 | 0.73 |
| F17 | -0.29 | 0.05 | 0.24 | 0.13 | 0.15 | 2.94 | 0.07 | 0 | 0.68 |
| F18 | -0.29 | 0.04 | 0.25 | 0.14 | 0.15 | 2.94 | 0.08 | 0 | 0.67 |
| F19 | -0.3 | 0.04 | 0.26 | 0.14 | 0.15 | 2.94 | 0.08 | 0 | 0.66 |
| F20 | -0.29 | 0.03 | 0.26 | 0.14 | 0.14 | 3.13 | 0.08 | 0 | 0.62 |
| F21 | -0.31 | -0.05 | 0.27 | 0.14 | 0.16 | 2.78 | 0.07 | 1 | 0.6 |
Table 3: Redox potential values of the quantum and molecular descriptors at SWN/6-31G level of approximation for the learning set
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F1 | -0.29 | -0.06 | 0.23 | 0.18 | 0.12 | 4.17 | 0.14 | 0 | 1.23 |
| F2 | -0.29 | -0.06 | 0.23 | 0.18 | 0.12 | 4.17 | 0.14 | 0 | 1.17 |
| F3 | -0.29 | -0.06 | 0.23 | 0.18 | 0.12 | 4.17 | 0.14 | 0 | 1.09 |
| F4 | -0.29 | -0.06 | 0.23 | 0.18 | 0.12 | 4.17 | 0.14 | 0 | 1.06 |
| F5 | -0.3 | -0.08 | 0.22 | 0.19 | 0.11 | 4.55 | 0.16 | 0 | 1.04 |
| F6 | -0.33 | -0.08 | 0.25 | 0.21 | 0.13 | 3.85 | 0.17 | 0 | 0.97 |
| F7 | -0.29 | -0.09 | 0.2 | 0.19 | 0.1 | 5 | 0.18 | 0 | 0.96 |
| F8 | -0.3 | -0.08 | 0.22 | 0.19 | 0.11 | 4.55 | 0.16 | 0 | 0.94 |
| F9 | -0.32 | -0.08 | 0.24 | 0.2 | 0.12 | 4.17 | 0.17 | 0 | 0.93 |
| F10 | -0.3 | -0.08 | 0.22 | 0.19 | 0.11 | 4.55 | 0.16 | 0 | 0.89 |
| F11 | -0.31 | -0.07 | 0.24 | 0.19 | 0.12 | 4.17 | 0.15 | 1 | 0.89 |
| F12 | -0.31 | -0.06 | 0.25 | 0.19 | 0.13 | 3.85 | 0.14 | 0 | 0.87 |
| F13 | -0.31 | -0.07 | 0.24 | 0.19 | 0.12 | 4.17 | 0.15 | 0 | 0.85 |
| F14 | -0.31 | -0.09 | 0.22 | 0.2 | 0.11 | 4.55 | 0.18 | 1 | 0.84 |
| F15 | -0.32 | -0.09 | 0.23 | 0.22 | 0.12 | 4.17 | 0.2 | 1 | 0.81 |
| F16 | -0.3 | -0.09 | 0.21 | 0.2 | 0.11 | 4.55 | 0.18 | 0 | 0.73 |
| F17 | -0.29 | -0.08 | 0.21 | 0.19 | 0.11 | 4.55 | 0.16 | 0 | 0.68 |
| F18 | -0.3 | -0.09 | 0.21 | 0.2 | 0.11 | 4.55 | 0.14 | 0 | 0.67 |
| F19 | -0.34 | -0.08 | 0.26 | 0.21 | 0.13 | 3.85 | 0.17 | 0 | 0.66 |
| F20 | -0.29 | 0.03 | 0.26 | 0.14 | 0.14 | 3.13 | 0.08 | 0 | 0.62 |
| F21 | -0.31 | -0.05 | 0.27 | 0.14 | 0.16 | 2.78 | 0.07 | 1 | 0.6 |
Table 4: Redox potential values of the quantum and molecular descriptors at HF/6-31G level of approximation for the learning set
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F1 | -0.39 | -0.05 | 0.34 | 0.22 | 0.17 | 2.94 | 0.94 | 0 | 1.23 |
| F2 | -0.37 | -0.02 | 0.35 | 0.2 | 0.18 | 2.78 | 0.11 | 0 | 1.17 |
| F3 | -0.35 | -0.01 | 0.34 | 0.18 | 0.17 | 2.94 | 0.1 | 0 | 1.09 |
| F4 | -0.35 | -0.01 | 0.34 | 0.18 | 0.17 | 2.94 | 0.1 | 0 | 1.06 |
| F5 | -0.35 | -0.02 | 0.33 | 0.19 | 0.17 | 2.94 | 0.11 | 0 | 1.04 |
| F6 | -0.35 | -0.01 | 0.34 | 0.18 | 0.17 | 2.94 | 0.1 | 0 | 0.97 |
| F7 | -0.35 | -0.01 | 0.34 | 0.18 | 0.17 | 2.94 | 0.1 | 0 | 0.96 |
| F8 | -0.35 | 0 | 0.35 | 0.18 | 0.18 | 2.78 | 0.09 | 0 | 0.94 |
| F9 | -0.35 | 0 | 0.35 | 0.18 | 0.18 | 2.78 | 0.09 | 0 | 0.93 |
| F10 | -0.34 | 0.01 | 0.35 | 0.17 | 0.18 | 2.78 | 0.08 | 0 | 0.89 |
| F11 | -0.35 | -0.01 | 0.34 | 0.17 | 0.17 | 2.94 | 0.09 | 1 | 0.89 |
| F12 | -0.34 | 0.01 | 0.35 | 0.17 | 0.18 | 2.78 | 0.08 | 0 | 0.87 |
| F13 | -0.33 | 0.02 | 0.35 | 0.16 | 0.18 | 2.78 | 0.07 | 0 | 0.85 |
| F14 | -0.34 | 0.01 | 0.35 | 0.17 | 0.18 | 2.78 | 0.08 | 1 | 0.84 |
| F15 | -0.33 | 0.01 | 0.34 | 0.16 | 0.17 | 2.94 | 0.08 | 1 | 0.81 |
| F16 | -0.35 | 0 | 0.35 | 0.18 | 0.18 | 2.78 | 0.09 | 0 | 0.73 |
| F17 | -0.32 | 0.02 | 0.34 | 0.15 | 0.17 | 2.94 | 0.07 | 0 | 0.68 |
| F18 | -0.32 | 0.01 | 0.33 | 0.16 | 0.17 | 2.94 | 0.08 | 0 | 0.67 |
| F19 | -0.33 | 0.01 | 0.34 | 0.16 | 0.17 | 2.94 | 0.08 | 0 | 0.66 |
| F20 | -0.32 | 0 | 0.32 | 0.16 | 0.16 | 3.13 | 0.08 | 0 | 0.62 |
| F21 | -0.34 | -0.02 | 0.36 | 0.16 | 0.18 | 2.78 | 0.07 | 1 | 0.6 |
Table 5: Redox potential values of the quantum and molecular descriptors at AM1 level for the learning set
The calculated values of the quantum descriptors at SWN/6-31G, HF/6-31G and AM1 theory level of the learning set and their redox potentials identified in the literature are summarized (Tables 6-8).
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F22 | -0.36 | -0.07 | 0.29 | 0.2 | 0.15 | 2.94 | 0.94 | 0 | 0.58 |
| F23 | -0.34 | -0.05 | 0.29 | 0.18 | 0.16 | 2.78 | 0.11 | 2 | 0.58 |
| F24 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 2 | 0.56 |
| F25 | -0.32 | -0.04 | 0.28 | 0.16 | 0.15 | 2.94 | 0.1 | 1 | 0.54 |
| F26 | -0.32 | -0.04 | 0.33 | 0.17 | 0.15 | 2.94 | 0.11 | 1 | 0.53 |
| F27 | -0.32 | -0.04 | 0.34 | 0.16 | 0.15 | 2.94 | 0.1 | 1 | 0.52 |
| F28 | -0.32 | -0.04 | 0.34 | 0.16 | 0.15 | 2.94 | 0.1 | 1 | 0.46 |
| F29 | -0.32 | -0.03 | 0.35 | 0.16 | 0.16 | 2.78 | 0.09 | 1 | 0.48 |
| F30 | -0.32 | -0.03 | 0.35 | 0.16 | 0.16 | 2.78 | 0.09 | 0 | 0.41 |
| F31 | -0.31 | 0.04 | 0.35 | 0.15 | 0.16 | 2.78 | 0.08 | 0 | 0.36 |
Table 6: Redox potential values of the quantum and molecular descriptors at SVWN/6-31G level of the test set
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F22 | -0.3 | -0.13 | 0.17 | 0.22 | 0.09 | 5.55 | 0.27 | 0 | 0.58 |
| F23 | -0.31 | -0.1 | 0.21 | 0.21 | 0.11 | 4.55 | 0.2 | 2 | 0.58 |
| F24 | -0.31 | -0.12 | 0.19 | 0.22 | 0.11 | 4.55 | 0.22 | 2 | 0.56 |
| F25 | -0.3 | -0.08 | 0.22 | 0.19 | 0.11 | 4.55 | 0.16 | 1 | 0.54 |
| F26 | -0.31 | -0.12 | 0.21 | 0.22 | 0.11 | 4.55 | 0.22 | 1 | 0.53 |
| F27 | -0.3 | -0.13 | 0.17 | 0.22 | 0.09 | 5.55 | 0.27 | 1 | 0.52 |
| F28 | -0.3 | -0.13 | 0.17 | 0.22 | 0.09 | 5.55 | 0.27 | 1 | 0.46 |
| F29 | -0.31 | -0.13 | 0.18 | 0.22 | 0.09 | 5.55 | 0.27 | 1 | 0.48 |
| F30 | -0.31 | -0.12 | 0.19 | 0.22 | 0.11 | 4.55 | 0.2 | 0 | 0.41 |
| F31 | -0.31 | -0.11 | 0.2 | 0.21 | 0.1 | 5 | 0.22 | 0 | 0.36 |
Table 7: Redox potential values of the quantum and molecular descriptors at SVWN/6-31G level of the test
| Code | Quantum descriptors | Molecular descriptor | Redox potential | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Gap | χ | η | S | ω | nOH | E | |
| F22 | -0.4 | -0 .05 | 0.3 | 0.2 | 0.2 | 3 | 1 | 0 | 0.58 |
| F23 | -0.4 | -0.02 | 0.4 | 0.2 | 0.2 | 3 | 0 | 2 | 0.58 |
| F24 | -0.4 | -0.01 | 0.3 | 0.2 | 0.2 | 3 | 0 | 2 | 0.56 |
| F25 | -0.4 | -0.01 | 0.3 | 0.2 | 0.2 | 3 | 0 | 1 | 0.54 |
| F26 | -0.4 | -0.02 | 0.3 | 0.2 | 0.2 | 3 | 0 | 1 | 0.53 |
| F27 | -0.4 | -0.01 | 0.3 | 0.2 | 0.2 | 3 | 0 | 1 | 0.52 |
| F28 | -0.4 | -0.01 | 0.3 | 0.2 | 0.2 | 3 | 0 | 1 | 0.46 |
| F29 | -0.4 | 0 | 0.4 | 0.2 | 0.2 | 3 | 0 | 1 | 0.48 |
| F30 | -0.4 | 0 | 0.4 | 0.2 | 0.2 | 3 | 0 | 0 | 0.41 |
| F31 | -0.3 | 0.01 | 0.4 | 0.2 | 0.2 | 3 | 0 | 0 | 0.36 |
Table 8: Redox potential values of the quantum and molecular descriptors at AM1 level of the test set
Verification of the dependency of variables: Two thirds (2/3) of the molecules (21 molecules) from the database were used for the development of models (training set and the 10 remaining will be used for the verification of models [12-16] (Table 9).
| SVWN/6-31G | HF/6-31G | AM1 | ||||
|---|---|---|---|---|---|---|
| Equations | Correlation coefficient linear lRl | Descriptor rejected if lRl<0.50 | Correlation coefficient linear lRl | Descriptor rejected if lRl<0.50 | Correlation coefficient linear lRl | Descriptor rejected if lRl<0.50 |
| E and EHOMO | 0.72 | Retained | 0.64 | Retained | 0.84 | Retained |
| E and ELUMO | 0.56 | Retained | 0.56 | Retained | 0.62 | Retained |
| E and Gap | 0.09 | Rejected | 0.23 | Rejected | 0.05 | Rejected |
| E and χ | 0.79 | Rejected | 0.64 | Retained | 0.86 | Retained |
| E and η | 0.04 | Rejected | 0.13 | Rejected | 0.07 | Rejected |
| E and S | 0.12 | Rejected | 0.34 | Rejected | 0.09 | Rejected |
| E and ω | 0.43 | Rejected | 0.28 | Rejected | 0.49 | Rejected |
| E and nOH | 0.37 | Rejected | 0.32 | Rejected | 0.27 | Rejected |
Table 9: Selection of quantum descriptors by criterion 1
Criteria Verification 1
Analysis of the results in Table 9 allows us to remember that for the SVWN/6-31G level of approximation, descriptors selected are: energy of the LUMO (ELUMO) and electronegativity (χ).
Analysis of the results in Table 9 allows us to remember that for the HF/6-31G level of approximation, descriptors selected are: energy of the LUMO (ELUMO) and electronegativity (χ).
Analysis of the results in Table 9 allows us to remember that for the AM1 level of approximation, descriptors selected are: Energy of the HOMO (EHOMO), energy of LUMO (ELUMO) and electronegativity (χ) [17].
Application of criterion 2: Definitive selection of quantum descriptors.
The results of definitive selection of quantum descriptors at SWN/6-31G, HF/6-31G and AM1 level are shown in Table 10.
| Correlation between: | Coefficient | Descriptors independent if<0.70 |
|---|---|---|
| EHOMO and ELUMO | 0.79 | Dependent |
| EHOMO and χ | -0.83 | Independent |
| ELUMO and χ | -0.68 | Independent |
Table 10: Definitive selection of quantum descriptors at SWN/6-31G level
Analysis of the results in Table 10 shows that the descriptors: energy of the LUMO (ELUMO) and the energy of HOMO (EHOMO) are dependent on each other. They cannot belong to the same group. Hence one needs to consider two groups of predictive quantum descriptors [18]. The two groups of quantum descriptors are as follows (Table 11)
| Correlation between | Coefficient | Descriptors independent if<0.70 |
|---|---|---|
| EHOMO and ELUMO | 0.79 | Dependent |
| EHOMO and χ | -0.71 | Independent |
| ELUMO and χ | -0.88 | Independent |
Table 11: Definitive selection of quantum descriptors at HF/6-31G level
Group 3: LUMO energy (ELUMO) and electronegativity (χ).
Group 4: HOMO energy (EHOMO) and electronegativity (χ)
Analysis of the results in Table 11 shows that the descriptors: energy of the LUMO (ELUMO) and the energy of HOMO (EHOMO) are dependent on each other. They cannot belong to the same group. Hence one needs to consider two groups of predictive quantum descriptors [19] (Table 12). The two groups of quantum descriptors are as follows:
| Correlation between | Coefficient | Descriptors independent if< 0.70 |
|---|---|---|
| EHOMO and ELUMO | 0.84 | Dependent |
| EHOMO and χ | -0.95 | Independent |
| ELUMO and χ | -0.82 | Independent |
Table 12: Definitive selection of quantum descriptors at AM1 level
Group 5: LUMO energy (ELUMO) and electronegativity (χ)
Group 6: HOMO energy (EHOMO) and electronegativity (χ)
Analysis of the results in Table 12 shows that the descriptors: energy of the LUMO (ELUMO) and the energy of HOMO (EHOMO) are dependent on each other. They cannot belong to the same group. Hence one needs to consider two groups of predictive quantum descriptors. The two groups of quantum descriptors are as follows:
Group 1: LUMO energy (ELUMO) and electronegativity (χ)
Group 2: HOMO energy (EHOMO) and electronegativity (χ)
QSPR models of antioxidant properties: From learning set and predictive descriptors selected, we established a QSPR model of the redox potential E. To choose the group that will be used to establish the regression equation of the QSPR model, the Fisher coefficients of the two groups will be compared and then the most significant group in Fisher's sense will be used [20].
Model regression equation: The Fisher coefficients for groups 3 and 4 are provided by the ANOVA tables in Tables 13 and 14.
| DS | SC | MSC | F1 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 0.51 | 0.42 | 17.23 | 0.000011 |
| 18 | 0.61 | 0.12 | |||
| 20 | 0.113 |
Table 13: ANOVA table of SWN/6-31G level quantum descriptors for group 3
| DS | SC | MSC | F2 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 0.84 | 0.24 | 92.46 | 0.000015 |
| 18 | 0.72 | 0.01 | |||
| 20 | 0.153 |
Table 14: ANOVA table of SWN/6-31G level quantum descriptors for group 4
Analysis of the results in Tables 13 and 14 shows that the Fisher coefficient (F2) of group 4 is greater than the Fisher coefficient (F1) of group 4: F1<F2; this means that the group 4 regression equation will be more significant than that of group 3. Group 4 quantum descriptors can therefore be meaningful in redox potential QSPR model establishing at SWN/6-31G level. The results of the multi-linear regression obtained from descriptors of group 4 are shown in Table 15.
| DS | SC | MSC | F1 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 16313,77 | 32,62,753 | 42,61,446 | 0.0003 |
| 16 | 29023,16 | 22,32,551 | |||
| 18 | 45336,93 |
Table 15: ANOVA table of AM1 level quantum descriptors for group1
The Fisher coefficients for groups 5 and 6 are provided by the ANOVA tables in Tables 15 and 16.
| DS | SC | MSC | F2 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 11056,65 | 22,11,329 | 0,8378 | 0,0546 |
| 16 | 34310,79 | 26,39,292 | |||
| 18 | 45367,44 |
Table 16: ANOVA table of AM1 level quantum descriptors for group 2
Analysis of the results shows that the Fisher coefficient (F2) of group 6 is greater than the Fisher coefficient (F1) of group 5: F1<F2; this means that the group 6 regression equation will be more significant than that of group 5. Group 6 quantum descriptors can therefore be meaningful in redox potential QSPR model establishing at HF/6-31G level [21]. The results of the multi-linear regression obtained from descriptors of group 6 are shown in Table 16.
The Fisher coefficients for groups 1 and 2 are provided by the ANOVA tables in Tables 17 and 18.
| DS | SC | MSC | F1 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 0.47 | 0.23 | 26.32 | 0.000005 |
| 18 | 0.16 | 0.01 | |||
| 20 | 0.63 |
Table 17: ANOVA table of AM1 level quantum descriptors for group 1
| DS | SC | MSC | F2 | P-value | |
|---|---|---|---|---|---|
| Regression residual total | 2 | 0.48 | 0.24 | 29.64 | 0.000002 |
| 18 | 0.14 | 0.01 | |||
| 20 | 0.63 |
Table 18: ANOVA table of AM1 level quantum descriptors for group 2
Analysis of the results in Tables 17 and 18 shows that the Fisher coefficient (F2) of group 2 is greater than the Fisher coefficient (F1) of group 1: F1<F2; this means that the group 2 regression equation will be more significant than that of group 1. Group 2 quantum descriptors can therefore be meaningful in redox potential QSPR model establishing at AM1 level. The results of the multi-linear regression obtained from descriptors of group 2 are shown in Table 19.
| Constants | Coefficients | Ecart-type | Test t | P-value |
|---|---|---|---|---|
| -2.21 | 0.67 | -1.46 | 0.15 | |
| ELUMO | -1.3 | 2.47 | -0.45 | 0.65 |
| χ | 10.24 | 4.42 | 2.37 | 0.09 |
Table 19: Regression coefficients value of group 3 for model
Regression equation of the model is: E=-2, 21-1, 3 ELUMO+10, 24 χ
ANOVA table of the model that allowed analysis of the variance. This ANOVA table indicates that the p-value (0.000011) is less than α=0.05 showing that the equation model regression is significant in redox potential predicting (Table 20).
| Constants | Coefficients | Standard deviation | Test t | P-value |
|---|---|---|---|---|
| -28.44 | 16.71 | -2.35 | 0.003 | |
| ELUMO | 52.01 | 40.83 | 0.36 | 0.072 |
| χ | -71.26 | 24.56 | -0.13 | 0.894 |
Table 20: Regression coefficients values of group 6 for model
Regression equation of the model is: E=-28.44-52.01ELUMO+71.26χ. The p-value (0.000002) is less than α=0.05 showing that the equation Model regression is significant in redox potential predicting (Table 21).
| Constants | Co-efficients | Standard deviation | Test t | P-value |
|---|---|---|---|---|
| -1.12 | 0.76 | -1.46 | 0.15 | |
| ELUMO | -1.93 | 4.27 | -0.45 | 0.65 |
| χ | 7.7 | 4.42 | 1.73 | 0.09 |
Table 21: Regression coefficients values of group 1 for model
Regression equation of the model is: E=-1.12 -1.93 ELUMO+7.70 χ
ANOVA table of the model that allowed analysis of the variance is that of Table 7. This ANOVA table indicates that the p-value (0.000002) is less than α=0.05 showing that the equation Model regression is significant in redox potential predicting.
Contribution of quantum descriptors in the prediction of redox potential E
The analysis of the results in Table 19-21 shows that
According to absolute values of the t-test in Table 19, the importance of the quantum descriptors of the SVWN/6- 31G level in the model is in the following ascending order: ELUMO<χ; Contribution calculations show that LUMO energy (ELUMO) contributes 10.54 in the prediction of the redox potential and the electronegativity (χ) has a contribution of 84.04. It is clear that electronegativity (χ) is the main descriptor predictive of the redox potential of these phenolic derivatives.
According to absolute values of the t-test in Table 20, the importance of the quantum descriptors of the HF/6-31G level in the model is in the following ascending order: χ<ELUMO Contribution calculations show that LUMO energy (ELUMO) contributes 73.46 in the prediction of the redox potential and the electronegativity (χ) has a contribution of 26.53. It is clear that energy (ELUMO) is the main descriptor predictive of the redox potential of these phenolic derivatives.
According to absolute values of the t-test in Table 21, the importance of the quantum descriptors of the AM1 level in the model is in the following ascending order: ELUMO< χ
Contribution calculations show that LUMO energy (ELUMO) contributes 20.64 in the prediction of the redox potential and the electronegativity (χ) has a contribution of 79.35. It is clear that electronegativity (χ) is the main descriptor predictive of the redox potential of these phenolic derivatives.
Statistical Parameters of the Model
Results for statistical parameters are shown in Table 22.
| Levels | n | R | R2 | R2aj | S | F | FIT |
|---|---|---|---|---|---|---|---|
| SVWN/6-31G | 21 | 0.47 | 0.22 | 0.43 | 0.078 | 17.23 | 0.67 |
| HF/6-31G | 21 | 0.98 | 0.96 | 0.83 | 0.087 | 4.26 | 0.76 |
| AM1 | 21 | 0.97 | 0.95 | 0.93 | 0.095 | 29.64 | 0.96 |
Table 22: Statistical parameters of the model
The analysis of the results in Table 22 shows that
For the SVWN/6-31G theory level,
The value of correlation coefficient R obtained (R=0.47) is lower than 1. This means that the redox potential is too weakly correlated with the variables energy of LUMO (ELUMO) and the electronegativity (χ).
The coefficient of determination obtained R2 indicates that the model does not have an explanatory power on the redox potential and that the descriptors have no effect on property explained.
Of all the above, the model cannot predict the potential. The x model is rejected.
For HF/6-31G theory level,
Analysis of data in Table 22 shows that redox potential is strongly correlated with quantum descriptors selected because of R-value of 0.98. In addition, 98% of experimental variance of redox potential is explained by the descriptors of the model. We can say that the model is validated and can be used as a model to predict the redox potential of molecules.
For AM1 theory level,
Data shows that redox potential is strongly correlated with quantum descriptors selected because of R-value of 0.97. In addition, 95% of experimental variance of redox potential is explained by the descriptors of the model 1. We can say that the model is validated and can be used as a model to predict the redox potential of molecules.
LOO Internal Validation of the Model,
The internal validation method applied in this study is cross-validation by omission of one molecule (in English Leave-One-Out: LOO). Cross validation LOO has been applied to the molecules of the learning game (Table 23).
| Interne | n | PRESS | Q2Loo | Spress | |
|---|---|---|---|---|---|
| 21 | 0.087 | 0.95 | 0.203 | ||
| Extern | n | R2ext | PRESS | Q2ext | SPRESS |
| 10 | 0.97 | 0.33 | 0.98 | 0.53 |
Table 23: Statistical parameters of the LOO internal and external validation of the model
The analysis of the results in Table 23 indicates that,
The model has a very high predictive power (QLoo2=0.95) because 95% of molecules in the learning game have their predicted redox potential.
The model has high predictive power (Q2ext=0.98) because 98.1% of the test set molecules has their predicted redox potential. In addition 97% of the experimental variance of the redox potential is explained by the quantum descriptors of the model (Table 24).
| Interne | N | PRESS | Q2Loo | Spress | |
|---|---|---|---|---|---|
| 19 | 0.082 | 0.92 | 0.103 | ||
| Extern | N | R2ext | PRESS | Q2ext | SPRESS |
| 10 | 0.99 | 0.19 | 0.94 | 0.31 |
Table 24: Statistical parameters of the LOO internal and external validation of the model
The analysis of the results in Table 24 indicates that
The model has a very high predictive power (QLoo^2=0.92) because 92% of molecules in the learning game have their predicted redox potential.
The model has high predictive power (Q2ext=0.94) because 94.1% of the test set molecules has their predicted redox potential. In addition 99% of the experimental variance of the redox potential is explained by the quantum descriptors of the model.
Verification of Tropsha's criteria for the model
At HF/6-31G level
• Rext2=0.85>0.70;
• Q2ext=0.71>0.60;
• (Rext2-R02)/(Rext2)=0.13>0.10 et 0.85< k<1.15;
• (Rext2-R0'2)/(Rext2)=0.03<0.10 et 0.85< k<1.15;
• | Rext2-R02 |=1.33>1.15.
We note that four of the five (3/5) the Tropsha criteria are verified. The model is therefore very efficient in the prediction of the redox potential E.
At HF/6-31G level
(1) Rext2=0.99>0.70;
(2) Q2ext =0.94>0.60
(3) (Rext2-R02)/(Rext2 )=0.05<0.10 et 0.85< k<1.15;
(4) (Rext2-R0'2)/(Rext2 )=0.05<0.10 et 0.85<k<1.15;
(5) | Rext2-R02 |=1.25>1.15.
We note that four of the five (4/5) the Tropsha criteria are verified. The model is therefore very efficient in the prediction of the redox potential E.
Normality Tests of the Model
At HF/6-31G level,
The results provided by the XLSTAT software are: Shapiro-Wilk test (Epred)
This test gives the following results: w=0.837; p-value=0.172; α=0.05
Test Interpretation: Since the calculated p-value is greater than the alpha threshold significance level (0.172>0.05), it is concluded that the predicted values of redox potential by the model follow a normal distribution.
Durbin-Watson test (residues),
This test gives the following results: U=0.787; p-value=0.266; α=0.05
Interpretation of the test: Since the calculated p-value is greater than the alpha threshold level of significance (0.787>0.05), it is concluded that the residues are not self-correlated. As result, they do not contain information that can influence the prediction of the model.
From different analyses of statistical tests, we can retain that the mode 1 established on the quantum descriptors: LUMO energy (ELUMO) and the electronegativity (χ) is validated and very powerful in the prediction of the redox potential. The regression equation of the prediction can be summarized as follows:
Prediction equation of the redox potential of model 1
E=-28.44-52.01ELUMO+71.26χ
n =31; R=0.98; R^2=0.96; Raj^2=0.83; S=0.087; F=4.26; FIT=0.76
At AM1 Level,
The results provided by the XLSTAT software are: Shapiro-Wilk test (Epred)
This test gives the following results: w=0.931; p-value=0.194; α=0.05
Test interpretation: Since the calculated p-value is greater than the alpha threshold significance level (0.194>0.05), it is concluded that the predicted values of redox potential by the model follow a normal distribution.
Durbin-Watson test (residues),
This test gives the following results: U=0.578; p-value=0.456; α=0.05
Interpretation of the test: Since the calculated p-value is greater than the alpha threshold level of significance (0.456>0.05), it is concluded that the residues are not self-correlated. As result, they do not contain information that can influence the prediction of the model.
From different analyses of statistical tests, we can retain that the model 2 established on the quantum descriptors: LUMO energy (ELUMO) and the electronegativity (χ) is validated and very powerful in the prediction of the redox potential. The regression equation of the prediction can be summarized as follows:
Prediction equation of the redox potential of model 2
E=-1.12-1.93 ELUMO+7.70 χ
n=31; R=0.97; R2=0.95; Raj2=0.93; S=0.095; F=29.64; FI =0.96
Correlation between calculated potential Epred and experimental Eexp
At HF/6-31G Level,
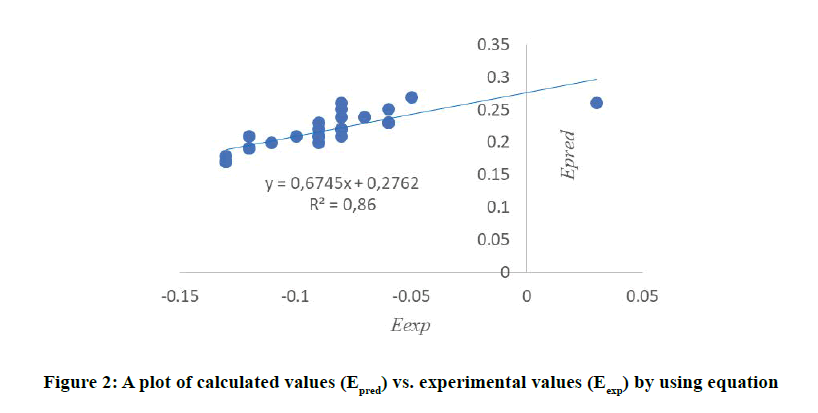
The curve in Figure 2 shows a strong linear correlation between predicted and experimental redox potentials. This graph confirms that the model 1 is validated and is very efficient in predicting redox potentials for this type of phenolic compounds (Figure 2).
n=31; R=0.98; R2=0.96; Raj2=0.83; S=0.087; F=4.26; FIT=0.76
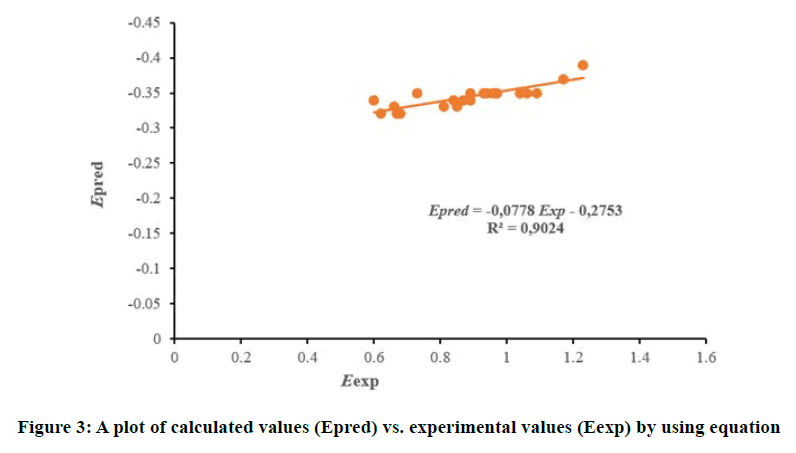
At AM1 Level,
The curve shows a strong linear correlation between predicted and experimental redox potentials. This graph confirms that the model 2 is validated and is very efficient in predicting redox potentials for this type of phenolic compounds (Figure 3).
E=-1.12-1.93 ELUMO+7.70 χ, with n=31, and R2=0.95.
Comparison of QSPR models for the prediction of redox potential established during this study
The purpose is to make a comparative study of the four QSPR models established in this study in order to obtain a classification of performance of these four models. Fisher coefficient is used to compare overall significance of the QSPR models established. The results are shown in Table 25.
| Models | Fisher coefficients (F) |
|---|---|
| Model 1: HF/6-31G | 4.26 |
| Model 2: (AM1) | 29.64 |
Table 25: Fisher coefficients of established models
Analysis of data in Table 25 shows that the most significant QSPR model in sense of Fisher is model 2 established because of its Fisher coefficient, which is the highest (F=29.64). On other hand, the least significant model is the model 1 established from the quantum descriptors at the HF/6-31G level of approximation because having the lowest coefficient of Fisher (F=4.26). We obtain this decreasing order of significance according to established models: Model 2>Model 1.
Conclusion
The QSPR methodology and quantum chemical methods were used to establish predictive models of redox potential of 31 phenolic derivatives. Two groups of quantum descriptors have been identified according to the basic criteria generally used. The results showed that the quantum descriptors: LUMO energy (ELUMO) and electronegativity (χ) correlated strongly with the redox potential of molecules. The statistical analysis allowed us to find two models explained by two equations: E=-1.12-1.93 ELUMO+7.70 χ and E=-28.44-52.01ELUMO+71.26χ obtained respectively from AM1 and HF/6-31G, which predict the redox potential with 95% and 98% confidence level respectively.
Acknowledgements
The calculations have been performed on the LACTHESMO Equipment of Professor Jean-Baptiste MENSAH at the University of Abomey-Calavi in Benin, and on PPMS at University of Lorraine. The authors would like to thank especially the PPMS (Pôle Messin de Modelisation et de Simulation) for providing us HPC resources.
References
- Rice-Evans CA, Diplock AT. Free Radic Biol Med. 1993; 15, 77- 96.
- Cadenas E, Packer L. J Phy Chem. 1996.
- Rice-Evans C A, Packer L. Free Radic Biol Med. 1998.
- Steenken S, Neta P. J Phys Chem. 1982; 86, 3661-3667.
- Jovanovic SV, Tosic M, Simic M G. J Phys Chem. 1991; 95, 10824-10827.
- Shertzer HG, Tabor MW, Hogan ITD, et al. Arch Toxicol. 1996; 70, 830-834.
- Van Acker SABE, de Groot MJ, Van den Berg D, et al. Chem Res Toxicol. 1996; 9, 1305-1312.
- Cao G, Sofic E, Prior R L. Free Radi Biol Med. 1997; 22, 749-760.
- Burton GW, Le Page Y, Gabe EJ, et al. J Am Chem Soc. 1980; 102, 7791-7792.
- Burton GW, Doba T, Gabe EJ, et al. J Am Chem Soc. 1985; 107, 7053-7056.
- Doba T, Burton GW, Ingold KU. J Am Chem Soc. 1983; 105, 6505-6506.
- Frisch MJ, Trucks GW, Schlegel HB, et al. Free Radi Biol Med. 2013.
- XLSTAT. Addinsoft. 2014.
- Partie de Microsoft Office. Professionnel Plus. 2013.
- Lien EJ, Ren S, Bui HH, et al. Free Radi Biol Med. 1999; 26, 285-294.
- Van Acker SABE, Koymans LMH, Bast A. Free Radi Biol Med. 1993; 15, 311-328.
- Rice-Evans CA, Packer L. J Phys Chem. 1998.
- Chabi Doco R, Kpota Houngue MTA, Gaston KA, et al. J Chem Pharma Res. 2017; 9(5), 231-236.
- Steenken S, Neta P. J Phys Chem. 1982; 86, 3661-3667.
- Jovanovic SV, Tosic M, Simic MG. J Phy Chem. 1991; 95, 10824-10827.
- Burton GW, Hughes L, Ingold KU. J Am Chem Soc. 1983; 105, 5950-5951.